最短的桥

934. 最短的桥

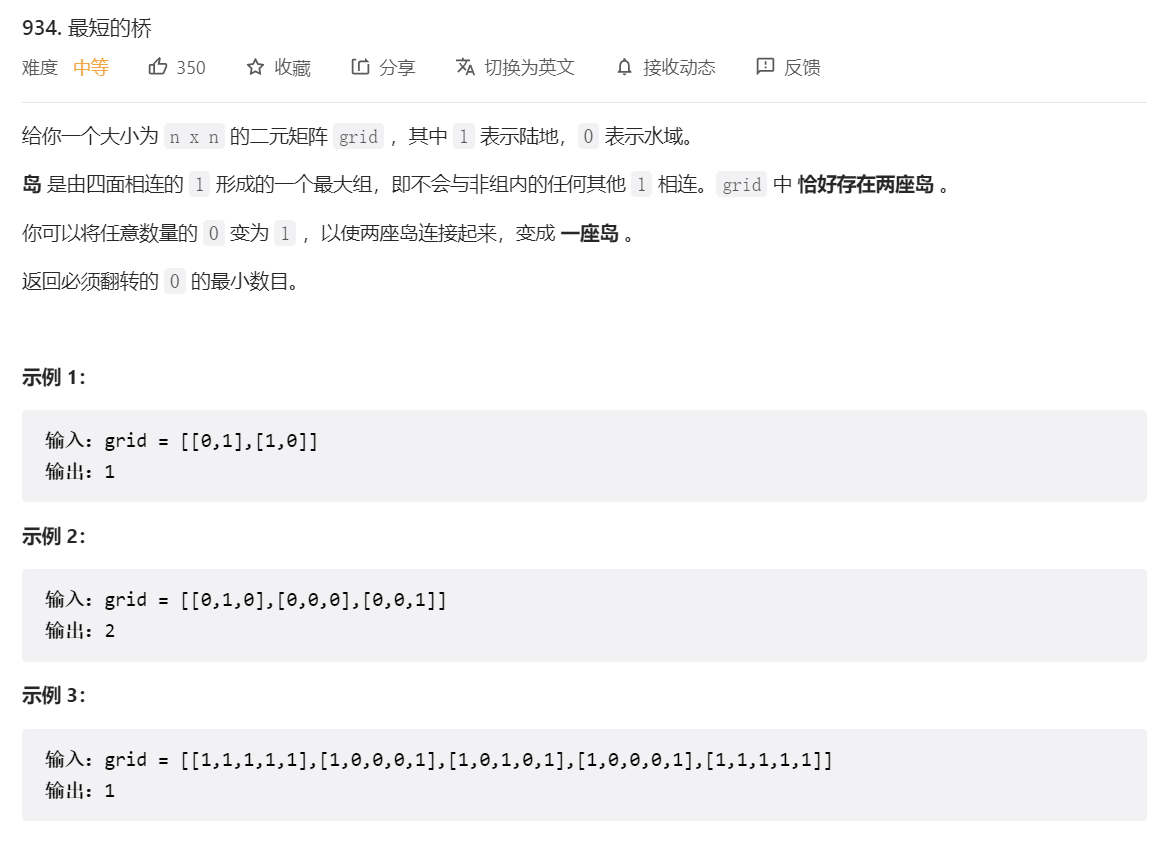
题目分析

下面是一个水域	左上角有一个岛	右下角有一个岛	找到两岛间的桥
0	1	0	0
1	1	0	0
0	0	0	1
0	0	1	1

大致想法：我们不需要将两个岛全部都找到，只需要找到第一个岛，然后从这个岛开始扩张，每次向外扩张一圈，直到找到第二个岛，那么我们的扩张次数就是这两个岛间的最短的桥了

逐步实现：
首先是如何找到第一个岛？

我们可以先使用广度优先算法：

• 首先遍历二维数组得到第一个 1 的位置（这就意味着我们摸到了第一个岛的一个角）

/**
 * @param {number[][]} grid
 * @return {number}
 */
var shortestBridge = function (grid) {
  for (let i = 0; i < edge; i++) {
    for (let j = 0; j < edge; j++) {
      if (grid === 1) {
        // 找到第一个岛
      }
    }
  }
};

• 找到这个岛之后，我们需要知道这个岛具体有多大？它的边界在哪里？

• 我们可以使用广度优先算法来找到这个岛的全貌：我们现在得到了这个岛的一个 1，将它放入一个“待搜查”队列 queue 中，对于 queue 队列中的每一个点我们搜查它周围所有的 1 ，新找到的 1 也放入 queue 队列，用完的 1 扔给 island 数组，直到 queue 中没有点排队了，这样我们就将整个岛都纳入 island 数组了。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var shortestBridge = function (grid) {
  let edge = grid.length; // 水域的边界
  let island = []; // 存放岛的数组
  let queue = []; //存放待搜查的点的队列
  let qlen; //队列的长度
  let help = [
    [1, 0],
    [-1, 0],
    [0, 1],
    [0, -1],
  ]; //帮助我们找到周围的点的数组
  let step = 0; //步数

  for (let i = 0; i < edge; i++) {
    for (let j = 0; j < edge; j++) {
      if (grid[i][j] === 1) {
        grid[i][j] = 2; //将找到的岛的点标记为2，以防止重复搜索
        qlen = queue.push([i, j]); //排队等待搜查
        whlie(qlen != 0); //若全搜查完毕就跳出循环
        {
          let check = queue.shift(); //取出排在最前面的点
          qlen--;
          let x = check[0];
          let y = check[1]; //保存
          island.push(check); //放入岛的数组中
          for (let k = 0; k < 4; k++) {
            //四次循环找上下左右的邻居
            let nbx = x + help[k][0];
            let nby = y + help[k][1]; //找到邻居的坐标
            //判断邻居是否在水域内，且是否为岛
            if (
              nbx >= 0 &&
              nby >= 0 &&
              nbx < edge &&
              nby < edge &&
              grid[nbx][nby] === 1
            ) {
              queue.push([nbx, nby]); //如果是就让去排队等待检查
              qlen++;
              grid[nbx][nby] = 2; //改变标记
            }
          }
        }
      }
    }
  }
};

• 通过这些工作，我们就找到了第一个岛，并把岛的所有点的坐标都存在了 island 数组中，接下来我们就可以开始扩张去找第二个岛了。

• 还是使用广度优先算法来扩张，每一次扩张遍历 island 数组，检查每一个点的四周，如果是水域，就将它划入岛的范围内，直到某一次扩张遇到了第二个岛，这时候我们扩张的次数就是最短的桥的长度了。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var shortestBridge = function (grid) {
  let edge = grid.length; // 水域的边界
  let island = []; // 存放岛的数组
  let queue = []; //存放待搜查的点的队列
  let qlen; //队列的长度
  let help = [
    [1, 0],
    [-1, 0],
    [0, 1],
    [0, -1],
  ]; //帮助我们找到周围的点的数组
  let step = 0; //步数

  for (let i = 0; i < edge; i++) {
    for (let j = 0; j < edge; j++) {
      if (grid[i][j] === 1) {
        grid[i][j] = 2; //将找到的岛的点标记为2，以防止重复搜索
        qlen = queue.push([i, j]); //排队等待搜查
        while (qlen != 0) {
          //若全搜查完毕就跳出循环
          let check = queue.shift(); //取出排在最前面的点
          qlen--;
          let x = check[0];
          let y = check[1]; //保存
          island.push(check); //放入岛的数组中
          for (let k = 0; k < 4; k++) {
            //四次循环找上下左右的邻居
            let nbx = x + help[k][0];
            let nby = y + help[k][1]; //找到邻居的坐标
            //判断邻居是否在水域内，且是否为岛
            if (
              nbx >= 0 &&
              nby >= 0 &&
              nbx < edge &&
              nby < edge &&
              grid[nbx][nby] === 1
            ) {
              queue.push([nbx, nby]); //如果是就让去排队等待检查
              qlen++;
              grid[nbx][nby] = 2; //改变标记
            }
          }
        }
        for (let n of island) {
          queue.push(n); //将岛的所有点都放入队列中
        }
        while (queue.length != 0) {
          //开始第二次广度优先搜索
          //在每一轮的扩张中队列的长度是不变的，新增的点需要在下一轮扩张中被检查
          let qlen = queue.length;
          for (let k = 0; k < qlen; k++) {
            //每一轮扩张
            let check = queue.shift();
            let x = check[0];
            let y = check[1];
            for (let l = 0; l < 4; l++) {
              //四次循环找上下左右的邻居
              let nbx = x + help[l][0];
              let nby = y + help[l][1];
              if (nbx >= 0 && nby >= 0 && nbx < edge && nby < edge) {
                if (grid[nbx][nby] === 1) {
                  //如果找到岛，直接返回次数
                  console.log(step + "===");
                  return step;
                } else if (grid[nbx][nby] === 0) {
                  //如果是水域，就将它划入岛的范围内
                  queue.push([nbx, nby]);
                  grid[nbx][nby] = 2;
                }
              }
            }
          }
          step++; //每一轮扩张结束后步数加一
        }
      }
    }
  }
};

总结

这一题中寻找第一个岛全部点还可以使用深度优先算法，有时间的时候可以尝试一下。

本题的广度优先思想使用了两次，一次是在获取所有岛的点，一次是在扩张岛的范围。两者有一个共同点： 虽说都是基于现有的点来计算，但是被计算的主体并不是 island 数组。究竟哪些点需要计算其周围的情况，是由 queue 队列来决定的。 这是控制时间与空间复杂度的关键。一个 queue 队列可以减少大量的重复运算。